Society For Neuroscience

Introduction. Two key issues in the cortical mapping of receptive field (RF) size are its population composition and its scaling with level in the visual hierarchy. Although it is well-established neurophysiologically that RF size spans only about a factor of 4 at any particular eccentricity (e.g. Gattass, Sousa & Rosa, 1987, J Comp Neurol), most computational models of visual processing operate on the assumption that there are channels of all sizes throughout the visual field. Conversely, in human vision, both electrophysiological (Tyler & Apkarian, 1981, New York Acad Sci) and psychophysical (Kontsevich & Tyler, 2015, J Vision) evidence suggests that there are two subpopulations of RF sizes in each local region of cortex, separated by about a factor of 3 in size (e.g., peaking at 3 arcmin and 9 arcmin in the fovea), with the sizes scaling with eccentricity.
Methods. An analysis of extrastriate receptive field (RF) data in macaque areas V2, V3 and V3A published posthumously in Hubel et al. (2013, Cereb Cortex), together with the original publication of V1 RF data (Hubel & Wiesel, 1974, J Comp Neurol), prompted a reanalysis of the RF sizes in the cortical (eccentricity-scaled) coordinate frame for the present study of RF size as a function of eccentricity and level in the cortical visual hierarchy.
Results. The distribution of eccentricity-scaled RF sizes was significantly bimodal in each cortical area, fitting a model of two discrete populations of RF sizes separated by about a factor of three. The size ranges for both sub-populations increased by about a log unit from V1 to V3A (reaching sizes of roughly 0.5 and 1.5 deg in foveal V3A, for example).
Conclusion. Thus, the reanalysis of these data pose a challenge to neural and computational models of extended object processing beyond their respective discrete sizes, implying that the local processing of spatial structure derives from the comparison of only two size signals, and that the mechanism for processing elongated or large stimuli in central vision must be deferred to the later stages of the visual hierarchy.

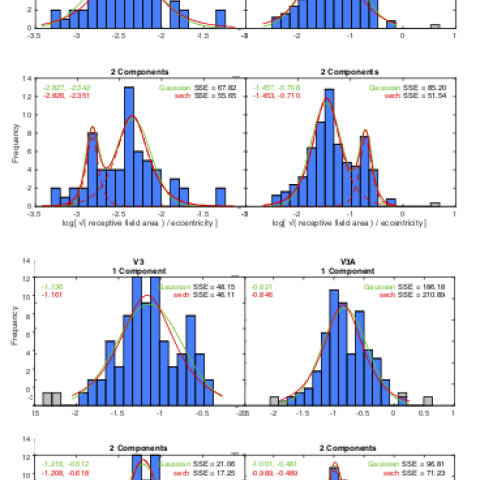
Figure:. Histograms of the distributions of receptive-field area scaled to eccentricity for V1 (from Hubel & Wiesel, 1974) and for V2, V3 and V3A (from Hubel, Wiesel and Conway, 2015). The histograms are fitted by four models of the distributions, single-component models (upper row) and two-component models (lower row).  Each model is fitted in the alternative forms of Gaussian components (green curves) and sech function components (red curves). For the two-component firs, the separate components for the sech model are plotted as dashed curves.

To characterize the data for each cortical area, histograms were constructed of the receptive field area scaled with eccentricity. To determine whether the distributions were significantly bimodal, the data were fitted by single- and two-component models of the distributions.   Because the data had noticeably long tails, the data were fitted by sech models in addition to the traditional Gaussian model, where the sech is defined as 

1/(ex+ e-x) and the Gaussian by e-(x2). The two-component models give substantially better fits than the single-component models. The two functions give similar fits for the single-component models, but the sech function gives significantly better fits than the Gaussian for the two-component models for all four cortical areas.

This analysis therefore provides strong support to the hypothesis that the receptive field areas conform to two distinct sub-populations both at each eccentricity and in each cortical area.  The distribution peaks are separated by about 0.5 log units, or a factor of 3 in linear receptive field size in each of the four cortical areas.

1.    Hubel DH, Wiesel TN, Yeagle EM, Lafer-Sousa R, Conway BR (2013) Binocular stereoscopy in visual areas V-2, V-3, and V-3A of the macaque monkey. Cerebral Cortex. 25(4):959-71.

2.    Hubel DH, Wiesel TN(1974) Sequence regularity and geometry of orientation columns in the monkey striate cortex. Journal of Comparative Neurology. 158(3):267-93.